
Aptitude questions and answers on Boats and Streams
1) The speed of a boat in still water is 5km/hr. If the speed of the boat against the stream is 3 km/hr, what is the speed of the stream?
- 1.5 km/hr
- 2 km/hr
- 2.5 km/hr
- 1 km/hr
The correct answer is B
Answer with explanation:
Let the speed of stream = X km/hr
Speed of boat = 5 km/hr
Speed upstream = 3km/hr
Apply formula: Speed upstream = speed of boat - speed of stream
∴ 3 = 5 - X
X = 5 - 3 = 2 km/hr
2) A man rows downstream at 20 km/hr and rows upstream at 15 km/hr. At what speed he can row in still water?
- 17.5 km/hr
- 18 km/hr
- 20.5 km/hr
- 22 km/hr
The correct answer is A
Apply formula: Speed in still water = 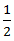 (speed downstream + speed upstream)
(speed downstream + speed upstream)
Speed downstream = 20 km/hr
Speed upstream = 15 km/hr
∴ Required speed = 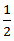 (20 + 15) km/hr
(20 + 15) km/hr
= 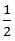 ∗ 35 = 17.5 km/hr
∗ 35 = 17.5 km/hr
3) A boat covers 800 meters in 600 seconds against the stream and returns downstream in 5 minutes. What is the speed of the boat in still water?
- 1 m/s
- 1.5 m/s
- 2 m/s
- 2.5 m/s
The correct answer is C
Answer with explanation:
Speed upstream = 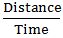 =
= 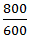 =
= 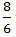 m/s
m/s
Speed downstream = 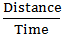 =
= 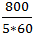 =
= 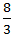 m/s
m/s
Apply formula: Speed in still water = 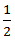 (speed downstream + speed upstream)
(speed downstream + speed upstream)
X = 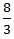 m/s
m/s
Y = 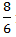 m/s
m/s
∴ Speed in still water = 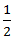
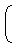
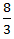 +
+ 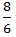
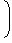
= 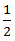 ∗ 4 = 2 m/s
∗ 4 = 2 m/s
4) A man can row a boat at a speed of 20 km/hr in still water. If the speed of the stream is 5 km/hr, in what time he can row a distance of 75 km downstream?
- 1.5 hours
- 2 hours
- 2.5 hours
- 3 hours
The correct answer is D
Answer with explanation:
Speed of boat = 20 km/hr
Speed of stream = 5 km/hr
∴ Speed downstream = 20 + 5= 25 km/hr
Required Time = 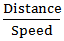 =
= 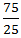 = 3 hours
= 3 hours
5) A man swimming in a river that is flowing at 3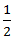 km/hr finds that in a given time he can swim twice as far downstream as he can swim upstream. What will be his speed in still water?
km/hr finds that in a given time he can swim twice as far downstream as he can swim upstream. What will be his speed in still water?
- 9.5 km/hr
- 10 lm/hr
- 10.5 km/hr
- 11 km/hr
The correct answer is C
Answer with explanation:
Let the man swims at X km/hr in still water.
As per the question, he covers twice the distance downstream as he covers upstream in a given time.
Distance = Speed ∗ Time
∴ Speed downstream ∗ Time = 2 (Speed upstream ∗ Time)
Time is the same in both cases.
∴ X+3 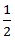 =2∗
=2∗ 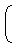 X - 3
X - 3 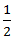
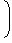
X + 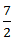 = 2∗
= 2∗ 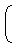 X -
X -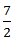
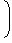
X + 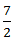 =2X - 7
=2X - 7
X-2X = -7 - 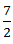
X = 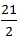 = 10.5 km/hr
= 10.5 km/hr
6) A man swimming in a river that is flowing at 3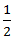 km/hr finds that in a given time he can swim twice as far downstream as he can swim upstream. What will be his speed in still water?
km/hr finds that in a given time he can swim twice as far downstream as he can swim upstream. What will be his speed in still water?
- 9.5 km/hr
- 10 lm/hr
- 10.5 km/hr
- 11 km/hr
The correct answer is C
Answer with explanation:
Let the man swims at X km/hr in still water.
As per the question, he covers twice the distance downstream as he covers upstream in a given time.
Distance = Speed ∗ Time
∴ Speed downstream ∗ Time = 2 (Speed upstream ∗ Time)
Time is the same in both cases.
∴ X+3 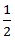 =2∗
=2∗ 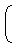 X - 3
X - 3 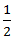
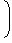
X + 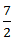 = 2∗
= 2∗ 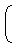 X -
X -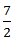
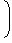
X + 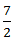 =2X - 7
=2X - 7
X-2X = -7 - 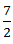
X = 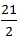 = 10.5 km/hr
= 10.5 km/hr
7) A man can row at 12 km/hr in still water. He finds that he takes twice as much time to row upstream than to row downstream when he covers a certain distance. Find the speed of the stream.
- 4 km/hr
- 3 km/hr
- 4.5 km/hr
- 3.5 km/hr
The correct answer is A
Answer with the explanation:
As per the quest ion, he takes twice the time when he rows upstream than rowing downstream.
Time is inversely proportioned to speed. So he rows at twice the speed when moving along the stream than moving against the stream.
Let his speed upstream = X km/hr
And, his speed downstream = 2X
∴ Speed in still water = 1/2 (2X+X) = 1.5 X km/hr
As per the question;
1.5X = 12 km/hr
X = 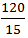 =8 km/hr
=8 km/hr
Speed upstream = 8 km/hr
So, speed downstream = 2 ∗ 8= 16 km/hr
Speed of current = 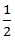 (speed downstream - speed upstream)
(speed downstream - speed upstream)
= 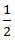 (16 - 8)
(16 - 8)
= 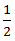 * 8 = 4 km/hr
* 8 = 4 km/hr
8) A boat takes 6 hours to move downstream from point P to Q and to return to point P moving upstream. If the speed of the stream is 4 km/hr and the speed of the boat in still water is 6 km/hr, what is the distance between point P and Q?
- 8 km
- 9 km
- 10 km
- 11 km
The correct answer is C
Answer with the explanation:
Let the distance between points P and Q = X km
Speed downstream = 6 + 4= 10 km/hr
Speed upstream = 6 - 4 = 2 km/hr
Time = 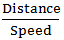
So, as per question;
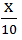 +
+ 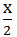 = 6 hours
= 6 hours
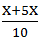 = 6
= 6
6X = 60
X = 10 km
9) A man can swim in still water at 8 km/hr. If the river is flowing at 2km/hr he takes 80 minutes to reach a place and return back, how far is the place?
- 4 km
- 3 km
- 4.5 km
- 5 km
The correct answer is D
Answer with the explanation:
Let the place is X km far.
Speed downstream = 8+2=10 km/hr
Speed upstream = 8 - 2 = 6 km/hr
Time = 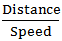
So, as per question;
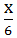 +
+ 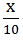 =
= 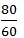
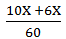 =
= 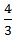
30X + 18X = 240
48X = 240
X = 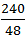 = 5 km
= 5 km
10) A motorboat travels 16 km in 2 hours against the flow of the river and travels the next 8 km along with the flow of the river in 20 minutes. How long will it take a motorboat to travel 48 km in still water?
- 2.5 hours
- 3 hours
- 3.5 hours
- 4 hours
The correct answer is B
Answer with the explanation:
Speed = 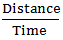
Speed upstream = 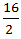 = 8 km/hr
= 8 km/hr
Speed downstream = 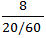 =
= 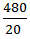 = 24 km/hr
= 24 km/hr
∴ Speed in still water = 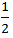 (speed downstream +speed upstream)
(speed downstream +speed upstream)
= 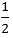 (24+8)=16 km/hr
(24+8)=16 km/hr
Required time = 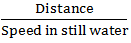
= 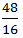 =3 hour
=3 hour
11) The velocity of a boat in still water is 9 km/hr, and the speed of the stream is 2.5 km/hr. How much time will the boat take to go 9.1 km against the stream?
- 1 hr. 20min
- 2hr. 40min
- 1hr. 24min
- 2hr. 48min
Answer: C
Answer with the Explanation:
ATQ,
Speed of boat in still water (Sb) = 9km/hr Speed of stream (Sc) = 2.5km/hr Distance against the stream = 9.1 km
Note: against the steam = upstream
Now, apply the formula:
The speed of boat upstream = speed of boat - the speed of the stream
The speed of upstream = 9-2.5 = 6.5km/hr Now, time= Distance/speed Time = 9.1/6.5, or 7/5 Or, time = 1[2/5] Or, 1hr + (2/5)*60 = 1hr + 24minutes
12) A man covers a distance of 36 km in 6 hours downstream and a distance of 40 km upstream in 8 hours. What is his speed in still water?
- 5.5km/hr
- 8km/hr
- 7km/hr
- None of these
Answer: A
Answer with the Explanation:
Upstream speed = distance covered in upstream/ time
Downstream speed = distance covered in downstream/ time
Upstream speed = 40/8 = 5kmph
Downstream speed = 36/6 = 6kmph
Now, speed of man in still water= (½) [speed in downstream + speed in upstream]
Or, the speed of man = [½][6+5] =5.5kmph
13) A boat travels upstream from Q to P and downstream from P to Q in 3 hours. If the distance between P to Q is 4km and the speed of the stream is 1kmph, then what is the velocity of the boat in still water?
- 3kmph
- 4kmph
- 5kmph
- 7.2kmph
Answer: A
Answer with the Explanation:
Let the velocity or speed of the boat in still water is x km/hr.
And the Speed of the stream = 1km/hr
So, the speed of the boat along the stream = (x+1) km/hr.
The speed of the boat against the stream = (x-1) km/hr.
Note: time = Distance / Speed
So, [4/ (x+1)] + [4/ (x-1)] = 3 hrs.
Note: go through the given options to get the answer quickly or solve the equation as follows:
Or, [4 (x+1+x-1)]/ [(x+1) (x-1)] = 3
Or, 8x = 3(x2-12)
Or, 8x = 3x2-3
Or, 3x2-8x-3=0
Or, 3x2- 9x+ x-3 = 0
Or, (x-3) (3x+1) = 0
Therefore x=3 or, x=-1/3 (speed can't be -ve)
Hence, the speed or velocity of the boat in still water is 3 km/hr.
14) The speed of the stream is 5km/hr. A boat goes 10 km upstream and returns back to the starting point in 50 minutes. Find the velocity of the boat in still water.
- 20km/hr
- 25km/hr
- 30km/hr
- 50km/hr
Answer: B
Answer with the Explanation:
Let the speed or velocity of the boat in still water is x km/hr
And the Speed of the stream = 5km/hr
So, the speed of the boat along the stream = (x+5) km/hr.
The velocity of the boat against the stream = (x-5) km/hr.
Note: Time = Distance / Speed
So, [10/ (x+5)] + [10/ (x-5)] = (50/60) hrs.
15) A boat travels from A to B along the stream and from B to A against the stream in 3 hours. If the velocity of the boat in still water is 4 km/hr, what is the distance between A and B?
- 8 km
- 10 km
- 12 km
- Data insufficient
Answer: D
Answer with the Explanation:
Let the distance between A and B is x km
The velocity of the boat in still water is 4km/hr.
Time taken to upstream and downstream is 3hr
Apply the formula:
Time = distance/speed
And Speed in the downstream = speed of the boat in still water+ speed of the stream
Speed in Upstream = speed of the boat in still water- speed of the stream
Let the speed of stream = y
So, (x/(4+y))+ (x/(4-y)) = 3hr.
We have one equation and two unknown expressions (x and y).
So, the given data is insufficient.
